martes, 22 de diciembre de 2015
FRACCIONES EQUIVALENTES
Fracciones equivalentes
Las fracciones equivalentes son aquellas fracciones que representan una misma cantidad.
lunes, 21 de diciembre de 2015
EL MÍNIMO COMÚN MÚLTIPLO EN LA SUMA DE FRACCIONESHETEROGENEAS

Fracciones heterogéneas
Una fracción o quebrado es la división de algo en partes . Si tomamos como ejemplo la fracción 2/4 se lee como dos cuartos, y lo que hace es señalar dos partes sobre las cuatro partes totales. Podemos observar entonces que lo que da nombre a esta fracción es el número de abajo el cual llamamos denominador ya que “denominamos” a la fracción como dos “cuartos”. El número superior de una fracción, que es el que se divide por el denominador se llama denominador. Tanto el numerador como el denominador son siempre números enteros, por lo cual las cifras que representan las fracciones son números racionales.
Vemos en el ejemplo anterior que en primer lugar se multiplicaron los denominadores, luego se realizó la multiplicación cruzada. Se sumaron los productos para obtener luego el numerador y finalmente se simplificó la fracción. Observemos otro ejemplo:
Podemos observar en este ejemplo que no fue necesario multiplicar entre si los denominadores, ya que 8 es múltiplo común tanto de 2 como de 4 así como de si mismo.
En la resta o sustracción de fracciones heterogéneas debemos utilizar las mismas reglas que usamos en la suma, lo único que cambia es que en este caso tenemos que restar en vez de sumar. Veamos un ejemplo:
En la multiplicación de fracciones, tanto fracciones homogéneas como heterogéneas se multiplican de igual forma. El producto de dos o más fracciones es entonces igual a otra fracción que tiene como numerador el producto de los numeradores y tiene también como denominador el producto de los denominadores. Veamos un claro ejemplo:
Dividamos fracciones heterogéneas o no, debemos cambiar siempre a una multiplicación y la segunda fracción cambiará entonces a su recíproco. El cociente de dos fracciones será otra fracción que tendrá como numerador el producto del numerador de la primera por el denominador de la segunda y tendrá por denominador el producto del denominador de la primera multiplicado por el denominador de la segunda.Veamos por último el siguiente ejemplo:
viernes, 18 de diciembre de 2015
RESTA DE FRACCIONES HETEROGENEAS
Cómo restar fracciones cuando tienen denominadores distintos? A esto se le llama resta de fracciones heterogéneas y es muy sencillo. Observa la siguiente infografía.
Resta de fracciones homogéneas
Para restar dos ó más fracciones homogéneas, se restan los numeradores y se deja el denominador común y simplificamos
Ejemplo:
Resta de fracciones heterogéneas
La resta de dos o más fracciones heterogéneas se realiza de la siguiente manera:
1. Se halla el mínimo común múltiplo de los dos denominadores:
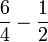 (mínimo común múltiplo de 4 y 2)
(mínimo común múltiplo de 4 y 2)
2. Se calculan los numeradores con la fórmula: numerador antiguo (6) x denominador común (4) y dividido por denominador antiguo (4)
( 6*4/4=6 )
Numerador antiguo (1) x denominador común (4) y dividido por denominador antiguo (2) ( 1*4/2= 2 )
3. Se procede como en la resta de fracciones de igual denominador (dado que las fracciones tienen el mismo denominador)
jueves, 17 de diciembre de 2015
suma de fracciones heterogeneas
PARA SUMAR FRACCIONES HETEROGÉNEAS:
Hallamos el mínimo común múltiplo de los denominadores. Luego ese valor lo dividimos para cada uno de los denominadores y lo multiplicamos por el respectivo numerador. Sumamos los totales, simplificamos y convertimos en número mixto. Ejemplo:
2 1 5 8 + 3 + 10 21 9
---- + --- + --- = --------------------- = ------- = 1-----
3 4 6 12 12 12
NOTA:
El mínimo común múltiplo es el menor número posible que se pueda dividir entre los denominadores de las fracciones.
Para transformar un fracción a número mixto dividimos el numerador para el denominador. Luego anotamos como número entero el cociente. El residuo como numerador y ubicamos el mismo denominador..
Hallamos el mínimo común múltiplo de los denominadores. Luego ese valor lo dividimos para cada uno de los denominadores y lo multiplicamos por el respectivo numerador. Sumamos los totales, simplificamos y convertimos en número mixto. Ejemplo:
2 1 5 8 + 3 + 10 21 9
---- + --- + --- = --------------------- = ------- = 1-----
3 4 6 12 12 12
NOTA:
El mínimo común múltiplo es el menor número posible que se pueda dividir entre los denominadores de las fracciones.
Para transformar un fracción a número mixto dividimos el numerador para el denominador. Luego anotamos como número entero el cociente. El residuo como numerador y ubicamos el mismo denominador..
 .
.
Notificar abuso
- Pulgar hacia arriba
- =
miércoles, 16 de diciembre de 2015
martes, 15 de diciembre de 2015
fracciones heterogeneas
FRACCIONES HETEROGÉNEAS
FRACCIONES HETEREOGÉNEAS
Dos fracciones son hetreogéneas cuando tiene distinto denominador.
Entre dos fracciones hetereogéneas con igual numerador es mayor la que tiene menor denominador
Ejemplo
9/8 y 9/5 9/5 > 9/8 porque 5<8
Ahora representemos gráficamente estas dos fracciones
9/8 < 9/5
Observa vamos a ordenar de mayor a menor las siguientes fracciones
1/5, 1/2, 1/6, 1/8, 1/10, 1/7, 1/9, 1/4
1/2> 1/4> 1/5 > 1/6 > 1/7 > 1/8 >1/9 < 1/10 porque 2<4<5<6 < 7<8<9 <10
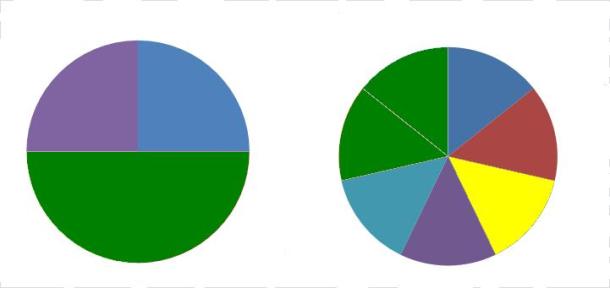
VAMOS A PRACTICAR Escriba el signo > o < según corresponda a) 13/9 13/7 b) 1/20 1/12 c) 7/4 7/2 d) 21/8 21/2 e) 3/6 3/9 e) 11/5 10/7 2) Escribe las fracciones según la siguiente grafica y dí cual es mayor y por qué
 3. Lee interpreta y soluciona
a) En una clase de Educación Física 1/8 de los estudiantes juegan fútbol, 1/6 juega baloncesto, y 1/3 practica el atletismo.¿Qué deporte prefieren los estudiantes?
b) Carlos compró cuatro pizzas para una fiesta y dividió cada una en 10 partes iguales. Al terminar la fiesta recogió los platos y vio que habían sobrado doce porciones.¿ Habría tenido suficiente con solo tres pizzas?
3. Lee interpreta y soluciona
a) En una clase de Educación Física 1/8 de los estudiantes juegan fútbol, 1/6 juega baloncesto, y 1/3 practica el atletismo.¿Qué deporte prefieren los estudiantes?
b) Carlos compró cuatro pizzas para una fiesta y dividió cada una en 10 partes iguales. Al terminar la fiesta recogió los platos y vio que habían sobrado doce porciones.¿ Habría tenido suficiente con solo tres pizzas?
lunes, 14 de diciembre de 2015
MAXIMO COMUN DIVISOR Y MINIMO COMUN MULTIPLO
Mínimo común múltiplo y máximo común divisor
Oir Lecc.
1.- Mínimo común múltiplo
Los múltiplos de un número se obtienen multiplicando el número por 1, 2, 3, 4...
Por ejemplo: los múltiplos de 4 son: 4, 8, 12, 16, 20, 24, 28...
El Mínimo Común Múltiplo (MCM) de 2 o más número es el menor de lo múltiplos comunes a estos números:
Por ejemplo: vamos a calcular el MCM de 3 y 4:
Múltiplos de 3: 3, 6, 9, 12, 15, 18, 21, 24...
Múltiplos de 4: 4, 8, 12, 16, 20, 24, 28...
Vemos que 12 es un múltiplo de ambos números y es el menor de los múltiplos comunes. Por lo tanto 12 es el Mínimo Común Múltiplo.
2.- Máximo común divisor
Los divisores de un número son aquellos que al dividir el número el resto es 0.
Por ejemplo: Divisores de 24 son: 1, 2, 3, 4, 6, 12 y 24.
Si se divide 24 por cualquiera de ellos el resto es 0.
El Máximo Común Divisor (MCD) de 2 o más número es el mayor de los divisores comunes a estos números:
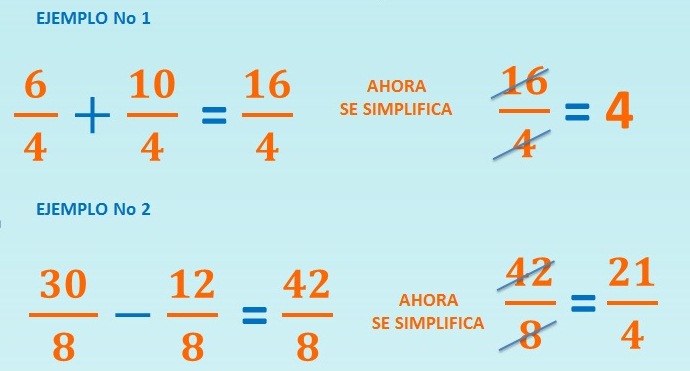
Por ejemplo: vamos a calcular el MCD de 30 y 42:
Divisores de 30: 1, 2, 3, 5, 6, 10, 15 y 30.
Divisores de 42: 1, 2, 3, 6, 7, 21 y 42.
Vemos que 6 es un divisor común a ambos números y es el mayor de los divisores comunes. Por lo tanto 6 es el Máximo Común Divisor.
viernes, 11 de diciembre de 2015
MINIMO COMUN MULTIPLO
En matemáticas, el mínimo común múltiplo (abreviado m.c.m), de dos o más números naturales es el menor número natural que es múltiplo común de todos ellos (o el ínfimo del conjunto de los múltiplos comunes). Este concepto ha estado ligado históricamente con números naturales, pero se puede usar para enteros negativos o enteros gaussianos.
Cálculo del mínimo común múltiplo (m.c.m)
Partiendo de 2 o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar todos los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:
|
|
|
Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:
Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.
Propiedades básicas
- Si a es un entero, entonces [a, a] = a
- Cuando a y b son enteros, [a, b] = b si, sólo si b es múltiplo de a.
- (a,b) = [a,b] si son iguales u opuestos.
- [a, b] = [ab] si, sólo si (a,b)= 1
- [a/d, b/d] = [m/a, m/b] donde m = mcm y d = mcd.2
- [ma,b]= m[a,b] si ([a,b]/a,m) = 13
- [a,b,c]= [[a,b], [b,c]]
- [a, b, c]|abc, donde abc ≠ 0
- [a,b,c] = abc (a,b,c)/(a,b)(b,c)(c,d)4
- Si el producto de dos números lo dividimos por su máximo común divisor dicho cociente es el mínimo común múltiplo.
- A y B que descompuestos en números primos será A=(p1·p2)·p3·p4 y B=(p1·p2)·p5·p6 donde si m.c.d. es (p1·p2) y el producto de A·B=(p1·p2)·p3·p4·(p1·p2)·p5·p6 donde vemos que (p1·p2) está repetido dos veces, luego si dividimos ese total por (p1·p2) tendremos el total menor que contiene a A y B siendo su mcm
- El mínimo común múltiplo de dos números, donde el menor divide al mayor, será el mayor. Es lógico ya que un múltiplo de ambos inferior al mayor sería imposible ya que no sería múltiplo del mayor.
- El mínimo común múltiplo de dos números primos es el total de su multiplicación. Esto es lógico ya que su máximo común divisor es 1.
- El mínimo común múltiplo de dos números compuestos será igual al cociente entre su producto y el m.c.d de ellos. Es evidente según la propiedad 1 de este tema.
- El máximo común divisor de varios números es un divisor del mínimo común múltiplo de tales números.
jueves, 10 de diciembre de 2015
EL MÁXIMO COMÚN DIVISOR

El máximo común divisor (m.c.d. o mcd) de dos o más números es el mayor número que divide a todos exactamente.
Cálculo del máximo común divisor
1 Se descomponen los números en factores primos.
2 Se toman los factores comunes con menor exponente.
3 Se multiplican dichos factores y el resultado obtenido es el mcd.
Ejemplo de cálculo de máximo común divisor
Hallar el m. c. d. de: 72, 108 y 60:
1 
Solución:
72 = 23 · 32
108 = 22 · 33
60 = 22 · 3 · 5
2 m. c. d. (72, 108, 60) = 22 · 3 = 12
12 es el mayor número que divide a 72, 108 y 60.
Propiedades del máximo común divisor
1 Los divisores comunes de varios números coinciden con los divisores del máximo común divisor.
Ejemplo:
Calcular los divisores comunes de 54 y 90.
m.c.d (54, 90) = 18
Los divisores comunes de 54 y 90 son los divisores de 18, por tanto serían 1, 2, 3, 6, 9, 18.
m.c.d (54, 90) = 18
Los divisores comunes de 54 y 90 son los divisores de 18, por tanto serían 1, 2, 3, 6, 9, 18.
2 Dados varios números, si se multiplican o dividen por otro número entonces su m.c.d también queda multiplicado o dividido por el mismo número.
Ejemplo:
m.c.d. (54, 90) = 18
Si multiplicamos los dos números por 3 queda:
Si multiplicamos los dos números por 3 queda:
54 · 3 = 162
90 · 3 = 270
m.c.d. (162, 270) = 54 = 18 · 3
3 Esta propiedad es consecuencia de la anterior: Dados varios números, si se dividen por su m.c.d los cocientes resultantes son primos entre sí (su m.c.d es 1).
Ejemplo:
m.c.d. (54, 90) = 18
54 : 18 = 3
90 : 18 = 5
m.c.d. (3, 5) = 1
4 Si un número es divisor de otro, entonces este es el m. c. d de los dos.
Ejemplo:
El número 12 es divisor de 36.
m.c.d. (12, 36) = 12
Suscribirse a:
Comentarios (Atom)




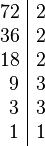
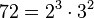
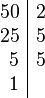

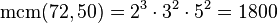
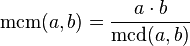
SUMA Y RESTA DE FRACCIONES HETEROGÉNEAS
Hay que reducir a común denominador.
1º Se calcula el m.c.m. de los denominadores. Descomponemos en factores
los denominadores y cogemos los factores comunes de mayor exponente y los no comunes.
2º Dividimos el m.c.m. obtenido entre cada uno de los denominadores y
lo que nos dé lo multiplicamos por el número que haya en el numerador.
3º Ya tenemos todas las fracciones con el mismo denominador, sumamos o restamos
los numeradores y dejamos el mismo denominador.
4º Si podemos simplificamos.
Ejemplos
Ejemplos
Ejemplos
FORMA ABREVIADA
SUMA DE FRACCIONES HETEROGENEAS