En matemáticas, una fracción, número fraccionario, (del vocablo latín frāctus, fractĭo -ōnis, roto, o quebrado)1 es la expresión de una cantidad dividida entre otra cantidad; es decir que representa un cociente no efectuado de números. Por razones históricas también se les llama fracción común, fracción vulgar o fracción decimal. El conjunto matemático que contiene a las fracciones es el conjunto de los números racionales, denotado ℚ.
De manera más general, se puede extender el concepto de fracción a un cociente cualquiera de expresiones matemáticas (no necesariamente números).
Numerador y denominador[editar]
Las fracciones se componen de: numerador, denominador y línea divisora entre ambos (barra horizontal u oblicua). En una fracción común 
el denominador "b" expresa la cantidad de partes iguales que representan la unidad, y el numerador "a" indica cuántas de ellas se toman.
el denominador "b" expresa la cantidad de partes iguales que representan la unidad, y el numerador "a" indica cuántas de ellas se toman.Representación gráfica y analítica[editar]
Suele utilizarse la figura geométrica (que representa la unidad) seccionada en una cantidad de partes iguales para mostrar el denominador, y se colorean (u omiten) las que se toman para distinguir la cantidad que indica el numerador.
- Notación y convenciones:
- En una fracción común, el denominador se lee como número partitivo (ejemplos: 1/4 se lee «un cuarto», 3/5 se lee «tres quintos»);
- Una fracción negativa se escribe con el signo menos delante de la fracción (ejemplos: -1/4 o
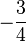, pero no 3/-4); - Una fracción genérica a/b representa el producto de a por el recíproco (multiplicativo) de b, de tal modo que
; si tanto a como b son números negativos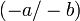 
, el producto es positivo, por lo que se escribe: a/b; - Toda expresión matemática escrita en esta forma recibe el nombre de «fracción».
La expresión genérica representa una división algebraica, por lo que el divisor debe ser distinto de cero (b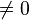 
); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
representa una división algebraica, por lo que el divisor debe ser distinto de cero (b 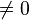); el cociente de esta división admite un desarrollo decimal (un número decimal, en el sistema de numeración decimal tradicional) que puede ser finito o infinito periódico (ver Número periódico).
Un número irracional no admite una escritura en forma de número fraccionario, o de razón, su expansión decimal será infinita no-periódica.
Algunos ejemplos de los que podemos mencionar son los valores de: "Pi", "El Número de Euler", "La Razón de Oro" y algunas raíces cuadradas y cúbicas.
Una fracción común representa un número racional, por lo que las fracciones comunes heredan todas las propiedades matemáticas de los racionales.
- Ejemplos
; 3/4; 3/4; (¾); fracción tres cuartos: numerador 3 y denominador 4, representa al número decimal 0.75, en porcentaje: 75%;
; fracción: numerador x² y denominador (x+3)(x-3), el valor decimal dependerá del valor de la variable x.
No hay comentarios:
Publicar un comentario