jueves, 21 de enero de 2016

ÁREA DE LOS CUATRILATEROS


ÁREA DEL RECTÁNGULO

La idea de que el área es la medida que proporciona el tamaño de la región encerrada en una figura geométrica proviene de la antigüedad. En el Antiguo Egipto, tras la crecida anual de río Nilo inundando los campos, surge la necesidad de calcular el área de cada parcela agrícola para restablecer sus límites; para solventar eso, los egipcios inventaron la geometría, según Heródoto.1
El modo de calcular el área de un polígono como la suma de las áreas de los triángulos, es un método que fue propuesto por primera vez por el sabio griego Antifón hacia el año 430 a. C. Hallar el área de una figura curva genera más dificultad. El método de agotamiento consiste en inscribir y circunscribir polígonos en la figura geométrica, aumentar el número de lados de dichos polígonos y hallar el área buscada. Con el sistema que se conoce como método exhaustivo de Eudoxo, consiguió obtener una aproximación para calcular el área de un círculo. Dicho sistema fue empleado tiempo después por Arquímedes para resolver otros problemas similares,2 así como el cálculo aproximado del   número π.

Área de un triángulo[editar]

Áreas en un plano cuadriculado.
  • El área de un triángulo es igual al semiproducto entre la longitud de una base y la altura relativa a esta:3
A=\frac{b\cdot h}{2}
donde b es la base del triángulo y h es la altura correspondiente a la base. (se puede considerar cualquier lado como base)
  • Si el triángulo es rectángulo, la altura coincide con uno de los catetos, con lo cual el área es igual al semiproducto de los catetos:
A=\frac{a\cdot b}{2}
donde a y b son los catetos.
A= \sqrt{s(s-a)(s-b)(s-c)}
donde a, b, c son los valores de las longitudes de sus lados, s = ½ (a + b + c) es el semiperimetro del triángulo.
A=\frac{\sqrt{3}\cdot a^2}{4}
donde a es un lado del triángulo.

Área de un cuadrilátero[editar]

Trapezoide.
  • El área del trapezoide o de cualquier cuadrilátero es igual al semiproducto de sus diagonales por el seno del ángulo que forman.
A= \frac {\overline{AC} \cdot \overline{BD} \cdot \sin \theta}{2}
El área también se puede obtener mediante triangulación:
A= \frac {a \cdot d \cdot \sin \alpha + b \cdot c \cdot \sin \gamma}{2}
Siendo:
\alpha\, el ángulo comprendido entre los lados a\, y d\,.
\gamma\, el ángulo comprendido entre los lados b\, y c\,.
  • El rectángulo es un paralelogramo cuyos ángulos son todos de 90º, y el área es igual al producto de dos de sus lados contiguos a y b:3
A = {a \cdot b \,}
  • El rombo es un paralelogramo, cuyos 4 lados son iguales, y tiene su área dada por el semiproducto de sus dos diagonales:
A = \frac{\overline{AC} \cdot \overline{BD}}{2}
  • El cuadrado es el polígono regular de cuatro lados; es a la vez un rectángulo y un rombo, por lo que su área puede ser calculada de la misma manera que la de estos dos. En particular, dado que sus lados son iguales, se usa la fórmula:3
A= a \cdot a \, = a^2
  • El romboide tiene su área dada por el producto de uno de sus lados y su altura respectiva:3
A= b\cdot h\,
  • El trapecio, el cual tiene dos lados opuestos paralelos entre sí y dos lados no paralelos, tiene un área que viene dada por la media aritmética de sus lados paralelos multiplicado por la distancia entre ellos (altura):3
A = \frac{a + b}{2} \cdot h
Publicado por en

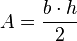
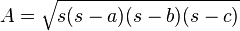
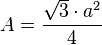
No hay comentarios:

Publicar un comentario

Suscribirse a: Enviar comentarios (Atom)