lunes, 29 de febrero de 2016
fracciones heterogeneas sumas y restas
SUMA Y RESTA DE FRACCIONES DE DIFERENTE DENOMINADOR
Hay que reducir a común denominador.
1º Se calcula el m.c.m. de los denominadores. Descomponemos en factores
los denominadores y cogemos los factores comunes de mayor exponente y los no comunes.
2º Dividimos el m.c.m. obtenido entre cada uno de los denominadores y
lo que nos dé lo multiplicamos por el número que haya en el numerador.
3º Ya tenemos todas las fracciones con el mismo denominador, sumamos o restamos
los numeradores y dejamos el mismo denominador.
4º Si podemos simplificamos.
Ejemplos
Ejemplos
Ejemplos
FORMA ABREVIADA
SUMA DE FRACCIONES HETEROGENEAS
RESTA DE FRACCIONES HETEROGENEAS
viernes, 26 de febrero de 2016
multiplicación y división de fracciones heterogeneas
División de Fracciones
Fórmulas para Recordar
Multiplicación de Fracciones
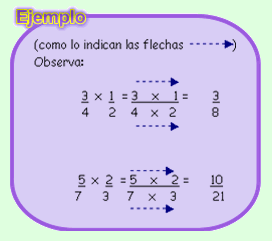
En la multiplicación de fracciones, las fracciones homogéneas y heterogéneas se multiplican de la misma forma:
Ejemplo: 2 · 3 = 6 =
3 4 12
^ Factorización Prima y simplificación
División de Fracciones
En la división de fracciones, siempre se cambia a multiplicación y la segunda fracción cambia a su recíproco.
Ejemplo:
3 ÷ 4 = 3 · 3 = 9
5 3 5 4 20
Ejemplo:
3 ÷ 1 = 3 · 2 = 6
7 2 7 1 7
Fórmulas para recordar
a + b = a + b Suma de Fracciones homogéneas
c c c
a + b = ad + bc Suma de Fracciones heterogéneas
c d cd
a - b = a - b Resta de Fracciones homogéneas
c c c
a - b = ad - bc Resta de Fracciones heterogéneas
c d cd
a · b = ab Multiplicación de Fracciones
c d cd
a ÷ b = a · d = ad División de Fracciones
c d c b cb
jueves, 25 de febrero de 2016
SUSTRACCION CON FRACCIONES HETEROGENEAS
La resta de fracciones es una operación aritmética por la que partiendo de dos fracciones se obtiene una tercera que es la diferencia entre ambas.
Resta de fracciones homogéneas[editar]
Para restar dos ó más fracciones homogéneas, se restan los numeradores y se deja el denominador común y simplificamos
Ejemplo:
Resta de fracciones heterogéneas[editar]
La resta de dos o más fracciones heterogéneas se realiza de la siguiente manera:
1. Se halla el mínimo común múltiplo de los dos denominadores:
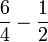(mínimo común múltiplo de 4 y 2)
2. Se calculan los numeradores con la fórmula: numerador antiguo (6) x denominador común (4) y dividido por denominador antiguo (4)
( 6*4/4=6 )
Numerador antiguo (1) x denominador común (4) y dividido por denominador antiguo (2) ( 1*4/2= 2 )
3. Se procede como en la resta de fracciones de igual denominador (dado que las fracciones tienen el mismo denominador)
miércoles, 24 de febrero de 2016
FRACCIONES HETEROGENEAS
FRACCIONES HOMOGENEAS Y HETEROGENEAS
FRACIONES HOMOGÉNEAS
Se llaman fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/4 y 5/4) si no comparten el denominador las llamamos fracciones heterogéneas.Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores y mantener igual el denominador. Veamos un ejemplo de esto:
En caso de realizar sustracciones o restas, procederemos de la misma forma que en una suma, pero en este caso estamos restando. Observemos un ejemplo:
FRACCIONES HETEROGÉNEAS
Se dice que dos fracciones son heterogéneas cuando estas poseen distinto denominador, por lo cual se diferencian de las fracciones homogéneas, que tienen el denominador en común. Si lo que queremos esrealizar sumas o restas con fracciones heterogéneas lo que debemos hacer en primer lugar, es encontrar el común denominador, o sea hallar el mínimo común múltiplo de todos los denominadores. Luego de esto lo que se debe hacer es colocar el denominador común, dividimos entonces el común denominador entre el primer denominador y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultadosobtenidos y así finalizamos. A veces no es necesario multiplicar entre si los denominadores, eso depende de las fracciones que tengamos. Veamos ahora un ejemplo de suma de fracciones heterogéneas bastante sencillo:
Vemos en el ejemplo anterior que en primer lugar se multiplicaron los denominadores, luego se realizó la multiplicación cruzada. Se sumaron los productospara obtener luego el numerador y finalmente se simplificó la fracción. Observemos otro ejemplo:
Se llaman fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/4 y 5/4) si no comparten el denominador las llamamos fracciones heterogéneas.Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores y mantener igual el denominador. Veamos un ejemplo de esto:
Se dice que dos fracciones son heterogéneas cuando estas poseen distinto denominador, por lo cual se diferencian de las fracciones homogéneas, que tienen el denominador en común. Si lo que queremos esrealizar sumas o restas con fracciones heterogéneas lo que debemos hacer en primer lugar, es encontrar el común denominador, o sea hallar el mínimo común múltiplo de todos los denominadores. Luego de esto lo que se debe hacer es colocar el denominador común, dividimos entonces el común denominador entre el primer denominador y el resultado lo multiplicamos por el numerador. Repetimos la operación con cada una de las fracciones que tengamos. Por último se suman los resultadosobtenidos y así finalizamos. A veces no es necesario multiplicar entre si los denominadores, eso depende de las fracciones que tengamos. Veamos ahora un ejemplo de suma de fracciones heterogéneas bastante sencillo:
martes, 23 de febrero de 2016
adicion y sustraccion con fracciones homogeneas
Fracciones homogéneas
En el campo de las matemáticas, una fracción o quebrado es la división de algo en partes. Si tomamos como ejemplo la fracción ¾ se lee como tres cuartos, y lo que hace es señalar tres partes sobre cuatro totales. Aquí podemos observar que lo que da nombre a esta fracción es el número de abajo el cual llamamos denominador ya que denominamos a la fracción como “tres cuartos”. El número superior de una fracción, que es el que se divide por el denominador lo llamamos numerador. Tanto el numerador como el denominador son siempre números enteros, por lo cual las cifras que representan las fracciones son números racionales.
Llamaremos fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/8 y 6/8) si no comparten el denominador las llamamos fracciones heterogéneas.Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores ymantener igual el denominador. Veamos un ejemplo de esto:
Llamaremos fracciones homogéneas a aquellas que comparten el mismo denominador por ejemplo (3/8 y 6/8) si no comparten el denominador las llamamos fracciones heterogéneas.Si realizamos una suma o adición de fracciones homogéneas, debemos sumar los numeradores y
En caso de realizar sustracciones o restas, procederemos de la misma forma que en una suma, pero en este caso estamos restando. Observemos un ejemplo:
En la multiplicación de fracciones homogéneas lo que debemos hacer es multiplicar por un lado el numerador y por otro lado el denominador. Debemos tener en cuenta que esto se aplica también a las fracciones heterogéneas, de esta forma obtenemos el producto. veamos a continuación una fórmula para esto:
El cociente de dos fracciones es otra fracción que tiene por numerador el resultado de la multiplicación de la primera por el denominador de la segunda, o sea el producto de esto, y tendrá como denominador el producto del denominador de la primera fracción por el numerador de la segunda. Llamaremos a esto, productos cruzados. Siempre se cambia a la multiplicación, y la segunda fracción cambia al recíproco. Esto no se aplica solamente a las fracciones homogéneas sino que también se aplica a las fracciones heterogéneas. Observemos a continuación la siguiente fórmula que nos dará el ejemplo:
L
viernes, 19 de febrero de 2016
fracciones homogeneas
FRACCIONES HOMOGÉNEAS
3/4 + 6/4 = 9/4
1/2 + 7/2 + 3/2 = 11/2
7/7 + 8/7 = 15/7
4/6 + 2/6 - 1/6 = 5/6
3/13 + 6/13 +8/13 = 17/13
FRACCIONES HETEROGENEAS
6 2 18 + 10 28
---- + --- = ------------- = ----------
5 3 15
9 2 2 27 - 4 - 8 15
---- - ----- - -- = ---------------- = ----
4 6 3 12 12
1 3 2 + 3 5
---- + ---- = --------------- = -----
2 4 4 4
7 1 14 - 1 13
---- + ---- = ------------ = --------
3 6 6 6
8 5 2 16 + 30 - 18 30
---- + --- - ----- = ------------------- = -------
9 3 2 18 18
jueves, 18 de febrero de 2016
SUMA Y RESTA CON FRACCIONES HOMOGÉNEAS.
Para sumar dos fracciones, hay que tener en cuenta de que existen 2 tipos de fracciones:
1. Fracciones homogéneas (1/4, 2/4, 9/4)
2. Fracciones heterogeneas (1/3, 2/5, 3/7)
Las fracciones homogéneas son las fracciones que tienen el mismo denominador; y las fracciones heterogeneas son las fracciones que tienen diferentes denominadores.
Suma de fracciones homogeneas
Las fracciones homogéneas, en suma, se suman los numeradores y el denominador se queda igual.
Ejemplos:
1/5 + 3/5 = 4/5
2/7 + 9/7 = 11/7
Suma de fracciones heterogéneas
Utilizando un algoritmo sencillo podemos aprender a sumar fracciones mentalmente.
Veamos: Sean a /b y c/d dos fracciones cualesquiera. Si las deseamos sumar podemos seguir la siguiente regla:
a/b + c/d = (ad + bc)/bd
se multiplica cruzado y los productos de suman / se multiplican los denominadores
Ejemplos:
1/4 + 1/3 = (1*3+4*1)/4*3 = (3+4)/12 = 7/12
1/3 + 2/5 = (1*5 + 3*2)/15 = (5+6)/15 = 11/15
1/4 + 1/2 = (2*1 + 4*1)/8 = 6/8
Simplificamos dividiendo por 2 numerador y denominador:
6/8 / 2/2 = 3/4
_______________________________________________________________________
Para restar dos fracciones, hay que tener en cuenta de que existen 2 tipos de fracciones:
1. Fracciones homogéneas (1/4, 2/4, 9/4)
2. Fracciones heterogeneas (1/3, 2/5, 3/7)
Las fracciones homogéneas son las fracciones que tienen el mismo denominador; y las fracciones heterogeneas son las fracciones que tienen diferentes denominadores.
Resta de fracciones homogeneas
Las fracciones homogéneas, en resta, se restan los numeradores y el denominador se queda igual.
Ejemplos:
7/5 - 3/5 = 4/5
12/7 - 9/7 = 3/7
Resta de fracciones heterogéneas
Utilizando un algoritmo sencillo podemos aprender a restar fracciones mentalmente.
Veamos: Sean a /b y c/d dos fracciones cualesquiera. Si las deseamos restar podemos seguir la siguiente regla:
a/b - c/d = (ad - bc)/bd
se multiplica cruzado y los productos de restan / se multiplican los denominadores
Ejemplos:
2/3 - 1/2 = (2*2 - 3*1)/6 = (4-3)/6 = 1/6
5/3 - 7/8 = (5*8 - 3*7)/24 = (40 -21)/24 = 19/24
19 es un número primo, con lo cual no podemos simplificar más la fracción.
Suscribirse a:
Entradas (Atom)