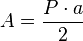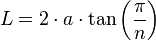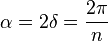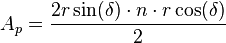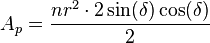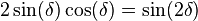jueves, 21 de abril de 2016

VIDEO DE LAS COORDENADAS DEL PLANO CARTESIANO

COORDENADAS EN EL PLANO CARTESIANO

Coordenadas cartesianas

Las coordenadas cartesianas se pueden usar para decir dónde estás exactamente en un mapa o gráfico

Coordenadas cartesianas

Con las coordenadas cartesianas señalas un punto en un gráfico dando la distancia de lado y hacia arriba:

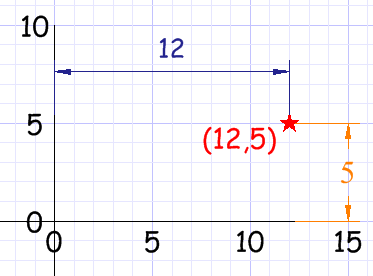El punto (12,5) está 12 unidades a la derecha y 5 arriba.

Ejes X e Y

La dirección izquierda-derecha (horizontal) se suele llamar X ... ... y arriba-abajo (vertical) se suele llamar Y. Las líneas de referencia (desde donde se miden distancias) se llaman ejes. Hay un eje X y un eje Y.
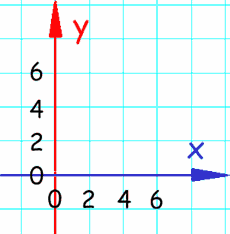	El eje X pasa por cero horizontalmente El eje Y pasa por cero verticalmente

Direcciones

	Cuando x (la primera coordenada) aumenta, el punto se mueve a la derecha. (Si disminuye, el punto va a la izquierda.)
	Cuando y (la segunda coordenada) aumenta, el punto se mueve arriba. (Si disminuye, el punto va abajo.)

Escribir coordenadas

Las coordenadas siempre se escriben en el mismo orden: la dirección horizontal primero, después la vertical. Esto se llama un "par ordenado".

Y normalmente los números se separan con una coma, y se rodean con paréntesis así: (3,2)

Ejemplo: (4,9) significa 4 unidades a la derecha y 9 arriba

Ejemplo: (0,5) significa 0 unidades a la derecha y 5 arriba. En otras palabras, sólo 5 unidades arriba.

Se llaman cartesianas porque las ideó el matemático y filósofo René Descartes a quien también se llamaba Cartesio. Es famoso por la frase "Pienso, luego existo".

Cuadrantes

¿Qué pasa cuando x o y es negativo? ¡Pues que empezamos en cero y vamos en la dirección contraria!

Esto significa que es posible tener combinaciones como x positivo e y negativo, o los dos negativos. De hecho hay cuatro combinaciones, y en un gráfico se llaman cuadrantes:

X (horizontal)	Y (vertical)	Ejemplo	Cuadrante
Positivo	Positivo	(3,2)	I
Negativo	Positivo	(-4,3)	II
Negativo	Negativo	(-2,-1)	III
Positivo	Negativo	(2,-3)	IV

La palabra cuadrante viene de cuad que significa cuatro. Por ejemplo, cuatro bebés que nacen a la vez se llaman cuatrillizos, y un animal de cuatro patas se llama cuadrúpedo)

Aquí tienes los cuatro cuadrantes en un gráfico:

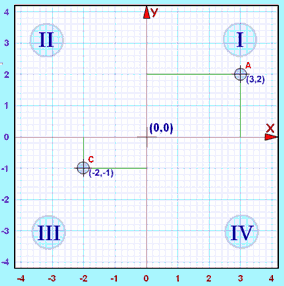Ejemplo: el punto "A" (3,2) está 3 unidades a la derecha y 2 arriba. Como x e y son positivos, el punto está en el "cuadrante I"

Ejemplo: el punto "C" (-2,-1) está 2 unidades horizontalmente en dirección negativa,
y 1 abajo (también dirección negativa). Como x e y son los dos negativos, el punto está en el "cuadrante III"

El origen

El punto (0,0) tiene el nombre especial de "el origen", y a veces se le llama con la letra "O".

Dimensiones: 1, 2, 3 y más...

Piensa en esto:

1	En la línea de números sólo se puede ir a izquierda o derecha, así que cualquier posición se indica con un número
2	Las coordenadas cartesianas indican direcciones izquierda-derecha y arriba-abajo, así cualquier posición se indica con dos números
3	¿Cómo señalamos un punto en el mundo real (como la punta de tu nariz)? Necesitamos indicar izquierda-derecha, arriba-abajo y delante-detrás, eso son tres números, ¡o 3 dimensiones!

Y se pueden usar coordenadas cartesianas para localizar puntos en 3 dimensiones como en este ejemplo:

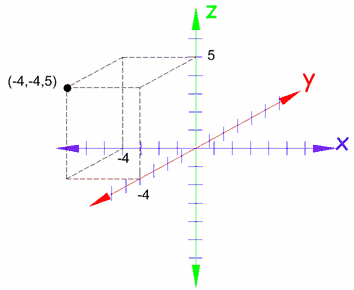Aquí el punto (-4,-4,5) se indica en coordenadas cartesianas tridimensionales.

miércoles, 20 de abril de 2016

ÁREA DEL POLÍGONOS REGULARES POR DESCOMPOSICIÓN EN TRIÁNGULOS.

ÁREA DE POLÍGONOS REGULARES POR DESCOMPOSICIÓN EN TRIÁNGULOS.

ÁREA DE POLÍGONOS REGULARES POR DESCOMPOSICIÓN EN TRIÁNGULOS

Un polígono regular es aquel cuyos ángulos $\alpha$ son iguales, y cuyos lados l tienen la misma longitud. El segmento que une el centro del polígono con el punto medio de cualquiera de sus lados es la apotema (a).

Uniendo el centro con cada uno de los vértices todo polígono regular de n lados se descompone en n triángulos iguales, los cuales serán isósceles, a excepción del hexágono regular en que serán equiláteros. La apotema es la altura de cada uno de dichos triángulos.

En un polígono regular de n vérices (y por lo tanto de n lados), los ángulos miden todos

(n-2) \cdot \frac {\pi}{n}

radianes, es decir

(n-2) \cdot \frac {180}{n}

grados (sexagesimales), lo que se obtiene muy fácilmente de la descomposición del polígono en triángulos: los ángulos de los n triángulos suman 180º n. Como los ángulos que convergen en el centro son en total 360º, resulta claro que los n ángulos $\alpha$ del polígono sumarán180ºn – 360º = 180º (n-2). Y, siendo dichos ángulos iguales, sólo habrá que dividir entre n para tener su valor. Desarrollándolo algebraicamente:

n \alpha+360^\circ=180^\circ n

n \alpha=180^\circ n-360^\circ=180^\circ \left(n-2 \right)

y finalmente,

\alpha=\left(n-2 \right)\frac{180^\circ}{n}

o bien,

\alpha=180^\circ-\frac{360^\circ}{n}

indistintamente.

Así, por ejemplo, para el triángulo (n = 3) -se trata de un triángulo equilátero-, los ángulos miden 1 x 180º/3 = 60º.

En el caso del cuadrilátero (n = 4) -un cuadrado-, los ángulos valen 2×180°/4 = 90°.

En cuanto a la superficie del polígono regular, es obvio que será n veces la de cada uno de los triángulos en que se ha descompuesto:

S=n \cdot \frac{base \cdot altura}{2}

pero siendo la base el lado l del polígono, y la altura su apotema a,

S=n \cdot \frac{l \cdot a}{2}

y finalmente, como

n \cdot l =\mbox {perímetro}

, nos queda

S=\frac{1}{2}\, \left( \mbox {perímetro}\cdot {apotema} \right )

Altura y apotema de un polígono regular, de número de lados > 4, cuyos ángulos sean iguales (y por tanto, su número sea par):

h=\frac{l}{A} + A \cdot l

a=\frac{h}{2}

l

, valor del lado del polígono.

h

, altura.

a

, apotema.

A

, resultado de la división de polígono, suma de ángulos de una de las figuras restantes y resta de 4 de Abel.

Para calcular

A

, se traza una línea que va desde el punto mitad de un lado hasta el punto mitad opuesto (o del lado opuesto), se cuentan los ángulos interiores de uno de los dos polígonos y se le resta 4.

En el caso de un hexágono (6 lados), se traza dicha línea que divide el polígono en 2 figuras. Dichas figuras, tienen cada una 5 ángulos convexos. Entonces, 5 - 4 = 1. Luego A = 1. En el caso de un octógono (8 lados), se traza dicha línea y se obtienen 2 figuras de 6 ángulos interiores cada una. 6 - 4 = A.

martes, 19 de abril de 2016

VIDEO DE LAS MEDIDAS DE MASAS

MEDIDAS DE MASA

lunes, 18 de abril de 2016

unidad de peso sistema internacional

la unidad de peso

El Sistema Internacional de Unidades, abreviado SI, es el sistema de unidades que se usa en todos los países del mundo, a excepción de tres que no lo han declarado prioritario o único.

Es el heredero del antiguo Sistema Métrico Decimal y por ello también se conoce como «sistema métrico».

Se instauró en 1960, en la XI Conferencia General de Pesas y Medidas, durante la cual inicialmente se reconocieron seis unidades físicas básicas. En 1971 se añadió la séptima unidad básica: el mol.

Una de las características trascendentales, que constituye la gran ventaja del Sistema Internacional, es que sus unidades se basan en fenómenos físicos fundamentales. Excepción única es la unidad de la magnitud masa, el kilogramo, definida como «la masa del prototipo internacional del kilogramo», un cilindro de platinoe iridio almacenado en una caja fuerte de la Oficina Internacional de Pesas y Medidas.^{nota 1}

Las unidades del SI constituyen referencia internacional de las indicaciones de los instrumentos de medición, a las cuales están referidas mediante una concatenación ininterrumpida de calibraciones o comparaciones.

Esto permite lograr equivalencia de las medidas realizadas con instrumentos similares, utilizados y calibrados en lugares distantes y, por ende, asegurar —sin necesidad de duplicación de ensayos y mediciones— el cumplimiento de las características de los productos que son objeto de transacciones en el comercio internacional, su intercambiabilidad.

Entre los años 2006 y 2009 el SI se unificó con las normas ISO para instaurar el Sistema Internacional de Magnitudes (ISO/IEC 80000, con las siglas ISQ).

Masa (M)	kilogramo (kg)^{nota 2}	Masa del prototipo internacional del kilogramo, adoptado por la Conferencia General de Pesas y Medidas y depositado en la Oficina Internacional de Pesas y Medidas, enSèvres, Francia. Este prototipo es un cilindro de 39 mm de altura y 39 mm de diámetro de una aleación90 % de platino y 10 % de iridio; tiene una densidad de 21 500 kg/m³.	Propuesta de redefinición a un valor relacionado con laconstante de Planck (h).

viernes, 15 de abril de 2016

área del polígono regular

area del poligono

Un polígono regular es un polígono con todos los lados y ángulos iguales.

Elementos del polígono regular

Existen varios elementos del polígono regular que los caracterizan.

Centro (C): es el punto del polígono regular que equidista a todos los vértices.
Lado (L): es uno de los n segmentos que delimitan el perímetro del polígono.
Vértice (V): punto de unión de dos lados. Existen tantos vértices como lados tiene el polígono (n).
Radio (r): es el segmento que une el centro con un vértice
Apotema (ap): segmento que une el centro con el punto medio de un lado. Laapotema es perpendicular a dicho lado.

Clasificación de polígonos regulares

Los polígonos regulares se pueden clasificar según el número de lados que tienen:

Triángulo equilátero: polígono con tres lados y ángulos iguales.
Cuadrado: polígono con cuatro lados y ángulos iguales.
Pentágono regular: polígono con cinco lados y ángulos iguales.
Hexágono regular: polígono con seis lados y ángulos iguales.
Heptágono regular: polígono con siete lados y ángulos iguales.
Octógono regular: polígono con ocho lados y ángulos iguales.
Eneágono regular: polígono con nueve lados y ángulos iguales.
Decágono regular: polígono con diez lados y ángulos iguales.
Undecágono regular: polígono con once lados y ángulos iguales.
Dodecágono regular: polígono con doce lados y ángulos iguales.

Apotema de un polígono regular

La apotema de un polígono regular puede obtenerse sabiendo el número de lados (N) del polígono y lo que mide cada lado (L).

Sea el ángulo central α el ángulo que forman las dos líneas que unen el centro delpolígono (O) y dos vértices consecutivos. Éste se calcula como:

Fórmula del ángulo central de un polígono regular

Mediante la tangente de la mitad del ángulo central y un lado (L), se calcula la apotema (ap) del polígono regular.

Fórmula de la apotema de un polígono regular

Área del polígono regular

El área de un polígono regular se calcula a partir de su perímetro y su apotema. Sea P el polígono regular con Nlados, su área es:

En un polígono regular, el perímetro se puede determinar por el producto del número de lados por la longitud de uno de los lados, es decir, Perímetro=N·L. O sea:

Dibujo de un polígono regular, sus lados y apotema para el cálculo de su área

miércoles, 13 de abril de 2016

estadística diagrama poligonal y circular

Polígonos de frecuencia

Un polígono de frecuencias se forma uniendo los extremos de las barras mediante segmentos.

También se puede realizar trazando los puntos que representan las frecuencias y uniéndolos mediante segmentos.

Ejemplo:

Las temperaturas en un día de otoño de una ciudad han sufrido las siguientes variaciones:

Hora	Temperatura
6	7º
9	12°
12	14°
15	11°
18	12°
21	10°
24	8°

El diagrama circular (también llamado diagrama de sectores o diagrama de pastel) sirve para representarvariables cualitativas o discretas. Se utiliza para representar la proporción de elementos de cada uno de los valores de la variable.

Consiste en partir el círculo en porciones proporcionales a la frecuencia relativa. Entiéndase como porción la parte del círculo que representa a cada valor que toma la variable.

Cálculo de los sectores

Un círculo completo son 360º (o 2π radianes). El ángulo de cada porción debe ser proporcional a la frecuencia de cada valor. Por ejemplo, si un valor representa un 50% del total de elementos, su sector del círculo tendrá un ángulo de 180º (o π radianes).

Sea (X₁,X₂,…,X_N) un conjunto de elementos. La fórmula para calcular el ángulo de cada sector es la siguiente:

Fórmula del ángulo de cada sector en grados sexagesimales del diagrama circular.

El ángulo de cada sector se calcula como 360º dividido por el total de sujetos (N) y multiplicado por la frecuencia absoluta (n_i), o bien el producto de la frecuencia relativa (f_i) por 360º. También podemos calcular el ángulo en radianes:

martes, 12 de abril de 2016

video el área del polígono regular

el área de polígonos regulares.

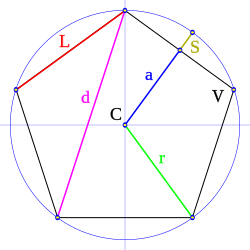
Elementos de un polígono regular

Lado, L: es cada uno de los segmentos que forman el polígono.
Vértice, V: el punto de unión de dos lados consecutivos.
Centro, C: el punto central equidistante de todos los vértices.
Radio, r: el segmento que une el centro del polígono con uno de sus vértices.
Apotema, a: segmento perpendicular a un lado, hasta el centro del polígono.
Diagonal, d: segmento que une dos vértices no contiguos.
Perímetro, P: es la suma de la medida de su contorno.
Semiperímetro, SP: es la semisuma del perímetro.
Sagita, S: parte del radio comprendida entre el punto medio del lado y el arco de circunferencia. La suma de la apotema: a más la sagita: S, es igual al radio: r.

Propiedades de un polígono regular

Los polígonos regulares son polígonos equiláteros, puesto que todos sus lados son de la misma medida.
Los polígonos regulares son equiangulares, puesto que todos sus ángulos interiores tienen la misma medida.
Los polígonos regulares se pueden inscribir en una circunferencia.

Área de un polígono regular[editar]

Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.

En función del perímetro y la apotema[editar]

El área de un polígono regular, conociendo el perímetro y la apotema es:

A = \frac {P \cdot a}{2}

[Expandir]Demostración

En función del número de lados y la apotema[editar]

Sabiendo que:

A_p = \frac {L \cdot n \cdot a} {2}

Además

\delta = \frac {\pi} {n} \

, ya que es la mitad de un ángulo central (esto en radianes).

Observando la imagen, es posible deducir que:

L = 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right )

Sustituyendo el lado:

A_p = \frac { \left ( 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right ) \right ) \cdot n \cdot a } {2}

Finalmente:

A_p = a^2 \cdot n \cdot \tan \left ( \frac {\pi} {n} \right )

Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.

En función del número de lados y el radio[editar]

Un polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que: