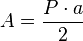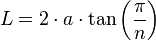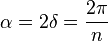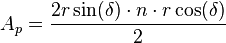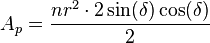jueves, 31 de marzo de 2016

VIDEO DE LAS EXPRESIONES DECIMALES

EXPRESIONES DECIMALES

Los números decimales pueden clasificarse en:

a) decimales finitos: son aquellos que tienen fin, es decir, no hay un número que se repita.

Ejemplos: 4,56 ; 0,0003 ; 2,9876 : 0,1 ; 3,42 , etc.

Siempre que se divida el numerador por el denominador, y la división termine y se obtenga resto cero, la división es exacta y su resultado será un decimal finito.

Un decimal finito representa una fracción decimal.

b) decimales infinitos: son aquellos números que no se acaban, es decir, hay uno o varios números que se repiten infinitamente. Por ejemplo: 0,333333..... es infinito por que el 3 se repite indefinidamente. Estos números son divisiones inexactas. No representan una fracción decimal.

Los decimales infinitos pueden ser: infinitos puros, infinitos periódicos e infinitos semiperiódicos.

Al conjunto de los números racionales sólo pertenecen los números decimales infinitos periódicos y semiperiódicos. Los decimales infinitos puros pertenecen al conjunto de los números irracionales, porque no pueden transformarse en fracción.

c) decimales infinitos periódicos: son aquellos que tiene una o más cifras que se repiten sucesiva e infinitamente, formando elperíodo. Se escribe en forma abreviada coronando al período con un pequeño trazo.

d) decimales infinitos semiperiódicos: En estos decimales aparecen una o más cifras antes del período. El número formado por dichas cifras se llama anteperíodo (es un número que está entre la coma y la rayita).

Transformación de un decimal finito a fracción

Se convierte el número a fracción decimal y, si se puede, se simplifica. Para transformar el número decimal a fracción decimal se utilizan potencias de diez (10, 100, 1.000, etc.). Se colocan tantos ceros como cifras decimales tenga el número.

Ejemplo 1:

$decimalafraccion02$

Se anota el número, en este caso 45. Se divide por 1.000, porque hay tres espacios decimales ocupados, luego simplificamos por 5

Ejemplo 2:

$decimalafraccion03$

Transformación de un decimal infinito periódico en fracción

Los pasos a seguir son los siguientes:

1) Se anota el número y se le resta él o los números que están antes del período (de la rayita)

2) Se coloca como denominador un 9 por cada número que está en el período (si hay un número bajo la rayita se coloca un 9, si hay dos números bajo el período se coloca 99, etc.). Si se puede simplificar, se simplifica.

Otro ejemplo: Expresar como fracción 57,18181818....

$decinmalafraccio01$

Transformación de decimal infinito semiperiódico a fracción

1) El numerador de la fracción se obtiene, al igual que en el caso anterior, restando al número la parte entera y el anteperíodo, o sea, todo lo que está antes de la “rayita”.

2) El denominador de la fracción se obtiene colocando tantos 9 como cifras tenga el período y tantos 0 como cifras tenga el anteperíodo. Como siempre, el resultado se expresa como fracción irreductible (no se puede simplificar más) o como número mixto.

miércoles, 30 de marzo de 2016

VIDEO DE LAS EXPRESIONES DECIMALES

EXPRESIONES DECIMALES

Fracciones decimales

Una fracción decimal es la que tiene como denominador a la unidad (1) seguida de ceros (10, 100, 1000, etc.).

$fracc_decimales1$

Notación decimal

Los décimos se escriben a la derecha del punto decimal. Si hay enteros se anotan a la izquierda del punto decimal y si no los hay se coloca un cero.

$fracc_decimales2$

Los centésimos ocupan hasta el segundo lugar a la derecha del punto.

$fracc_decimales3$

Los milésimos ocupan hasta el tercer lugar a la derecha del punto decimal.

$fracc_decimales4$

Y así se sigue con los diezmilésimos, cienmilésimos, millonésimos, etc.

Nomenclatura

Para leer un decimal se lee la parte entera si la hay y después la parte decimal dando el nombre de las unidades inferiores.

Ejemplo.

6.098 Se leen los enteros y como hay tres cifras después del punto, este lugar le corresponde a los milésimos. Por lo tanto este número se leerá así:

$fracc_decimales5$

Si son dos lugares a la derecha del punto, le corresponde a los centésimos.

$fracc_decimales6$

Si es sólo un lugar, serán décimos.

$fracc_decimales7$

Propiedades generales de las fracciones decimales

1.- Un decimal no se altera si se agregan o quitan ceros a la derecha, ya que su valor relativo no varía.

Ejemplo.

$fracc_decimales8$

Será lo mismo ya que 25 centésimos es igual a 250 milésimos y a 2500 diezmilésimos. En todos los casos el 2 es décimo y el 5 es centésimo.

2.- Si en un número decimal se recorre el punto decimal a la derecha uno o más lugares, el decimal queda multiplicado por la unidad seguida de tantos ceros como lugares se haya recorrido el punto a la derecha. Esto ocurre porque al correr el punto a la derecha un lugar, el valor relativo de cada cifra se hace diez veces mayor, luego el número queda multiplicado por 10; al correrlo dos queda multiplicado por 100; al correrlo tres queda multiplicado por 1000; etc. Si las cifras del número no son suficientes, se agregan ceros.

martes, 29 de marzo de 2016

las coordenadas en un plano cartesiano

las coordenadas en un plano

Las coordenadas cartesianas o coordenadas rectangulares (plano cartesiano) son un tipo de coordenadas ortogonales usadas enespacios euclídeos, para la representación gráfica de una función, en geometría analítica , o del movimiento o posición en física, caracterizadas porque usa como referencia ejes ortogonales entre sí que se cortan en un punto origen. Las coordenadas cartesianas se definen así como la distancia al origen de las proyecciones ortogonales de un punto dado sobre cada uno de los ejes. La denominación de 'cartesiano' se introdujo en honor de René Descartes, quien lo utilizó de manera formal por primera vez.

Si el sistema en sí es un sistema bidimensional, se denomina plano cartesiano. El punto de corte de las rectas se hace coincidir con el punto cero de las rectas y se conoce como origen del sistema. Al eje horizontal o de las abscisas se le asigna los números enteros de las equis ("x"); y al eje vertical o de las ordenadas se le asignan los números enteros de las yes ("y"). Al cortarse las dos rectas, dividen al plano en cuatro regiones o zonas, que se conocen con el nombre de cuadrantes:

Primer cuadrante "I": Región superior derecha
Segundo cuadrante "II": Región superior izquierda
Tercer cuadrante "III": Región inferior izquierda

circunferencia.
Cuarto cuadrante "IV": Región inferior derecha

El plano cartesiano se utiliza para asignarle una ubicación a cualquier punto en el plano. En la gráfica se indica el punto +2 en las abscisas y +3 en las ordenadas. El conjunto (2 , 3) se denomina "par ordenado" y del mismo modo se pueden ubicar otros puntos.

Las coordenadas cartesianas se usan por ejemplo para definir un sistema cartesiano o sistema de referencia respecto ya sea a un solo eje (línea recta), respecto a dos ejes (un plano) o respecto a tres ejes (en el espacio), perpendiculares entre sí (plano y espacio), que se cortan en un punto llamado origen de coordenadas. En el plano, las coordenadas cartesianas se denominan abscisa y ordenada. La abscisa es la coordenada horizontal y se representa habitualmente por la letra x, mientras que la ordenada es la coordenada vertical y se representa por la y.

Primer cuadrante "I": Región superior derecha
Segundo cuadrante "II": Región superior izquierda
Tercer cuadrante "III": Región inferior izquierda

circunferencia.
Cuarto cuadrante "IV": Región inferior derecha

Primer cuadrante "I": Región superior derecha
Segundo cuadrante "II": Región superior izquierda
Tercer cuadrante "III": Región inferior izquierda

circunferencia.
Cuarto cuadrante "IV": Región inferior derecha

lunes, 28 de marzo de 2016

VIDEO DIAGRAMA DE BARRAS

DIAGRAMA DE BARRAS

Un diagrama de barras, también conocido como gráfico de barras o diagrama de columnas, es una forma de representar gráficamente un conjunto de datos o valores, y está conformado por barras rectangulares de longitudes proporcionales a los valores representados. Los gráficos de barras son usados para comparar dos o más valores. Las barras pueden orientarse verticalmente u horizontalmente.

ste diagrama de ejemplo está basado en los resultados de la Elección del Parlamento Europeo en el 2004 y en el de 1999. La tabla siguiente lista el número de asientos asignadas a cada partido. Los resultados de 1999 han sido multiplicados por 1.16933, para compensar el cambio en el número de asientos entre estos años.

Grupo	Asientos (2004)	Asientos (1999) a escala
EURO	33	33 33	33
EFA	33	33	33	EDD	33	33	33	ELDR	67	60
EPP	276	272
UEN	27	36
Otros	66	29

Un gráfico de barras que represente los resultados anteriores de la elección del 2004 se vería así:
(Si todos los datos fuesen ordenados en orden descendiente, este tipo de gráfico de barras sería llamado un diagrama de Pareto.)

Este gráfico de barras muestra ambos resultados (2004 y 1999):

jueves, 17 de marzo de 2016

video diagrama de barras

diagrama de barras

Diagrama de barras

En estadística, un histograma es una representación gráfica de una variable en forma de barras, donde la superficie de cada barra es proporcional a la frecuencia de los valores representados, ya sea en forma diferencial o acumulada. Sirven para obtener una "primera vista" general, o panorama, de la distribución de la población, o la muestra, respecto a una característica, cuantitativa y continua, de la misma y que es de interés para el observador (como la longitud o la masa). De esta manera ofrece una visión en grupo permitiendo observar una preferencia, o tendencia, por parte de la muestra o población por ubicarse hacia una determinada región de valores dentro del espectro de valores posibles (sean infinitos o no) que pueda adquirir la característica. Así pues, podemos evidenciar comportamientos, observar el grado de homogeneidad, acuerdo o concisión entre los valores de todas las partes que componen la población o la muestra, o, en contraposición, poder observar el grado de variabilidad, y por ende, la dispersión de todos los valores que toman las partes, también es posible no evidenciar ninguna tendencia y obtener que cada miembro de la población toma por su lado y adquiere un valor de la característica aleatoriamente sin mostrar ninguna preferencia o tendencia, entre otras cosas.

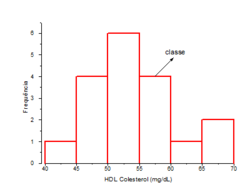
En el eje vertical se representan las frecuencias, es decir, la cantidad de población o la muestra, según sea el caso, que se ubica en un determinado valor o sub-rango de valores de la característica que toma la característica de interés, evidentemente, cuando este espectro de valores es infinito o muy grande el mismo es reducido a sólo una parte que muestre la tendencia o comportamiento de la población, en otras ocasiones este espectro es extendido para mostrar el alejamiento o ubicación de la población o la muestra analizada respecto de un valor de interés.

En general se utilizan para relacionar variables cuantitativas continuas, pero también se lo suele usar para variables cuantitativas discretas, en cuyo caso es común llamarlo diagrama de frecuencias y sus barras están separadas, esto es porque en el "x" ya no se representa un espectro continuo de valores, sino valores cuantitativos específicos como ocurre en un diagrama de barras cuando la característica que se representa es cualitativa o categórica. Su utilidad se hace más evidente cuando se cuenta con un gran número de datos cuantitativos y que se han agrupado en intervalos de clase.

Ejemplos de su uso es cuando se representan franjas de edades o altura de la muestra, y, por comodidad, sus valores se agrupan en clases, es decir, valores continuos. En los casos en los que los datos son cualitativos (no numéricos), como sexto grado de acuerdo o nivel de estudios, es preferible un diagrama de sectores.

Los histogramas son más frecuentes en ciencias sociales, humanas y económicas que en ciencias naturales y exactas. Y permite la comparación de los resultados de un proceso.

miércoles, 16 de marzo de 2016

VIDEO POLIGONOS REGULARES

POLÍGONOS REGULARES

En geometría, se denomina polígono regular a un polígono cuyos lados y ángulos interiores son congruentes entre sí. Los polígonos regulares de tres y cuatro lados se llaman triángulo equilátero y cuadrado, respectivamente. Para polígonos de más lados, se añade el término regular (pentágono regular, hexágono regular, octágono regular, etc). Solo algunos polígonos regulares pueden ser construidos con regla y compás.

Existen diversas fórmulas para calcular el área de un polígono regular, dependiendo de los elementos conocidos.

En función del perímetro y la apotema[editar]

El área de un polígono regular, conociendo el perímetro y la apotema es:

A = \frac {P \cdot a}{2}

[Expandir]Demostración

En función del número de lados y la apotema[editar]

Sabiendo que:

A_p = \frac {L \cdot n \cdot a} {2}

Además

\delta = \frac {\pi} {n} \

, ya que es la mitad de un ángulo central (esto en radianes).

Observando la imagen, es posible deducir que:

L = 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right )

Sustituyendo el lado:

A_p = \frac { \left ( 2 \cdot a \cdot \tan \left ( \frac {\pi} {n} \right ) \right ) \cdot n \cdot a } {2}

Finalmente:

A_p = a^2 \cdot n \cdot \tan \left ( \frac {\pi} {n} \right )

Con esta fórmula se puede averiguar el área con el número de lados y la apotema, sin necesidad de recurrir al perímetro.

En función del número de lados y el radio[editar]

Un polígono queda perfectamente definido por su número de lados n, y el radio r, por tanto podemos determinar cual es su área, a la vista de la figura, tenemos que:

L = 2 r \sin({\delta}) \;

a = r \cos({\delta}) \;

donde el ángulo central es:

\alpha = 2 \delta = \frac{2\pi}{n} \;

sabiendo que el área de un polígono es:

A_p = \frac{L \cdot n \cdot a}{2} \;

y sustituyendo el valor del lado y la apotema calculados antes, tenemos:

A_p = \frac{2 r \sin({\delta}) \cdot n \cdot r \cos({\delta})}{2} \;

ordenando tenemos:

A_p = \frac{n r^2 \cdot 2 \sin({\delta}) \cos({\delta})}{2} \;

sabiendo que:

2 \sin({\delta}) \cos({\delta}) = \sin({2 \delta}) \;

resulta:

A_p = \frac{n r^2 \sin({\alpha})}{2} \;

o lo que es lo mismo:

A_p = \frac{n r^2 \sin({\frac{2\pi}{n}})}{2} \;

Con esta expresión podemos calcular el área del polígono, conociendo solamente el número de lados y su radio, lo que resulta útil en muchos casos.

martes, 15 de marzo de 2016

VIDEO GRAFICAR FRACCIONES CON NUMEROS MIXTOS

TRAFICAR FRACCIONES CON NÚMEROS MIXTOS

Fracciones mixtas

	Definición rápida: una fracción mixta esun número entero y una fracción combinados, como 1 3/4.
1 3/4
(uno y tres cuartos)

Fracciones

Una fracción (como 3/4) tiene dos números:

Numerador

Denominador

Al número de arriba lo llamamos Numerador, es el número de partes que tenemos.
Al número de abajo lo llamamos Denominador, es el número de partes en que hemos dividido el total.

Hay tres tipos de fracciones:

Fracciones propias:	El numerador es menor que el denominador
Fracciones propias:	Ejemplos: 1/3, 3/4, 2/7

Fracciones impropias:	El numerador es mayor (o igual) que el denominador
Fracciones impropias:	Ejemplos: 4/3, 11/4, 7/7

Fracciones mixtas:	Un número entero y una fracción propia juntos
Fracciones mixtas:	Ejemplos: 1 1/3, 2 1/4, 16 2/5

Fracciones mixtas

Entonces, una fracción mixta es simplemente un númeo entero y una fracción combinadas en un número "mixto".

Fracciones mixtas = Fracciones impropias

Puedes usar una fracción impropia o una fracción mixta para escribir la misma cantidad. Por ejemplo 1 3/4 =7/4, aquí se ve :

1 3/4		7/4
	=

Cuándo se usan fracciones mixtas

En el uso cotidiano, la gente entiende mejor las fracciones mixtas. Es más fácil decir "me comí 2 1/4salchichas" que "me comí 9/4 salchichas".

Pero en matemáticas las fracciones impropias son mejores que las fracciones mixtas. Las fracciones mixtas se confunden cuando las escribes en una fórmula:

Fracción mixta:	¿Cuánto es:	1 + 2 1/4	?
	¿Es:	1+2+1/4	= 3 1/4 ?
	¿O es:	1 + 2 × 1/4	= 1 1/2 ?

Fracción impropia:	¿Cuánto es:	1 + 9/4	?
	Es:	4/4 + 9/4 = 13/4

Convertir fracciones impropias en fracciones mixtas

Para convertir una fracción impropia en mixta, sigue estos pasos:

Divide el numerador entre el denominador.
Escribe el cociente como un número entero.
Después escribe el resto encima del denominador.

Ejemplo: Convierte 11/4 en una fracción mixta.

Divide: 11 ÷ 4 = 2 con resto 3
Escribe el 2 y después escribe el resto (3) encima del denominador (4), así:

2	3

	4

Convertir fracciones mixtas en fracciones impropias

Para convertir una fracción mixta en impropia, sigue estos pasos:

Multiplica la parte entera por el denominador.
Súmalo al numerador.
Después escribe el resultado encima del denominador.

Ejemplo: Convierte 3 2/5 en fracción impropia.

Multiplica la parte entera por el denominador: 3 × 5 = 15
Súmalo al numerador: 15 + 2 = 17
Después escribe el resultado encima del denominador, así: