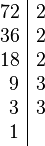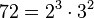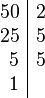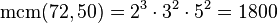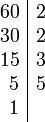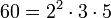VÍDEO DE MEDICIÓN DE ÁNGULOS SISTEMA SEXAGESIMAL

MEDICIÓN DE ÁNGULOS SISTEMA SEXAGESIMAL

. UNIDADES DE MEDIDAS DE ÁNGULOS. SISTEMA SEXAGESIMAL.

Para medir ángulos se necesitan dos cosas: Una unidad de medida. Un aparato que reproduzca dicha unidad de medida. Sistema sexagesimal: Recibe este nombre porque cada unidad es sesenta veces mayor (o menor) que la siguiente inferior (o superior). La unidad de medida de ángulos del sistema sexagesimal es el grado (º), que es el resultado de dividir el ángulo llano en 180 partes iguales. Así, un ángulo recto mide 90º. Cada grado se divide en 60 minutos (´) y, cada minuto, en 60 segundos (´´). Transportador de ángulos o semicírculo graduado. Es un semicírculo dividido en 180 partes iguales. Cada una de ellas es un grado (º).Las unidades que se usan para medir ángulos más pequeños que el grado son el minuto (1´) y el segundo (1´´). Sus equivalencias son 1º=60´ y 1´=60´´. El minuto y el segundo son unidades muy pequeñas que a simple vista no se aprecian. Para medirlas se utiliza el teodolito, un instrumento de mucha precisión. En la siguiente escena vamos a utilizar el transportador de ángulos para averiguar los grados (º) que mide un ángulo.

LOS TRIÁNGULOS Y SU CONTRUCCION

LOS TRIANGULOS COSTRUCCION

DEFINICIÓN Y CLASIFICACIÓN DE TRIÁNGULOS:

Un triángulo, es un polígono de tres lados; está formado por tres segmentos de recta que se denominan lados, o tres puntos no alineados que se llaman vértices.

La suma de los ángulos internos del triángulo siempre suman 180º.

Según sus lados se clasifican en:

• Triángulo equilátero: si sus tres lados tienen la misma longitud (los tres ángulos internos miden 60 grados)
• Triángulo isósceles: si tiene dos lados y dos ángulos iguales
• Triángulo escaleno: si todos sus lados y ángulos son distintos.

Según sus ángulos, pueden ser:

• Triángulo rectángulo: si tiene un ángulo interior recto (90°). A los dos lados que conforman el ángulo recto se les denomina catetos y al otro lado hipotenusa.
• Triángulo acutángulo: cuando sus tres ángulos son menores a 90°; el triángulo equilátero es un caso particular de triángulo acutángulo.
• Triángulo obtusángulo: si uno de sus ángulos es obtuso (mayor de 90°); los otros dos son agudos (menor de 90°).

VÍDEO LA RADICACION

LA RADICACION

En matemática, la raíz n-ésima de índice n de un número a es un número b, si existe, tal que bⁿ = a, donde n también se llama orden, a se denomina radicando. La notación a seguir tiene varias formas:

(1)

Para todo n > 1 natural, a y b reales positivos, se tiene la equivalencia:¹

a = bⁿ ⇔ b = ⁿ√a

La expresión  se llama radical, el símbolo  es el signo radical.²

La raíz de orden dos se llama raíz cuadrada y, por ser la más frecuente, se escribe sin índice: √x en vez de ²√x. La raíz de orden tres se llama raíz cúbica, ya que es la formula utilizada para averiguar los lados de un cubo, para otros casos se acude al nombre ordinal del orden, como raíz cuarta, quinta, etc.

Dentro de los números reales ℝ⁺ positivos, siempre puede encontrarse una única raíz enésima también positiva. Si el número a es negativo entonces sólo existirá una raíz real cuando el índice n sea impar.¹ La raíz enésima de un número negativo no es un número real (no está definida dentro de los números reales) cuando el índice n es par.

Dentro de los números complejos ℂ, para cada número z siempre es posible encontrar exactamente n raíces enésimas diferentes.

El cálculo efectivo de la raíz se hace mediante las funciones logaritmo y exponencial:

ⁿ√x = exp(^lnx/_n) = e^lnx/_n

Este método es empleado comúnmente en calculadoras de bolsillo y otro tipo de hardware.³ El problema es que dicho cálculo no funciona con los números negativos, porque el logaritmo usual sólo está definido en (0,+∞). De ahí una tendencia, todavía minoritaria, de restringir la definición de las raíces de orden impar ³√x, ⁵√x a los números positivos.

VIDEO LA POTENCIACION

LA POTENCIACION

La potenciación es una operación matemática entre dos términos denominados: base a y exponente n. Se escribe aⁿ y se lee usualmente como «a elevado a n» o «a elevado a la n» y el sufijo en femenino correspondiente al exponente n. Hay algunos números especiales, como el 2, al cuadrado o el 3, que le corresponde al cubo. Nótese que en el caso de la potenciación la base y el exponente pueden pertenecer a conjuntos diferentes, en un anillo totalmente general la base será un elemento del anillo pero el exponente será un número natural que no tiene porqué pertenecer al anillo. En un cuerpo el exponente puede ser un número entero.

VÍDEO DEL MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR

MÍNIMO COMÚN MÚLTIPLO Y MÁXIMO COMÚN DIVISOR

En matemáticas, el mínimo común múltiplo (abreviado m.c.m), de dos o más números naturales es el menor número natural que es múltiplo común de todos ellos (o el ínfimo del conjunto de los múltiplos comunes). Este concepto ha estado ligado históricamente con números naturales, pero se puede usar para enteros negativos o enteros 

Partiendo de 2 o más números y por descomposición en factores primos, expresados como producto de factores primos, su mínimo común múltiplo será el resultado de multiplicar todos los factores comunes y no comunes elevados a la mayor potencia, por ejemplo el mcm de 72 y 50 será:

Tomando los factores comunes y no comunes con su mayor exponente, tenemos que:

Conociendo el máximo común divisor de dos números, se puede calcular el mínimo común múltiplo de ellos, que será el producto de ambos dividido entre su máximo común divisor.

En matemáticas, se define el máximo común divisor(MCD) de dos o más números enteros al mayor número entero que los divide sin dejar resto.

Cálculo del MCD[editar]

Los tres métodos más utilizados para el cálculo del máximo común divisor de dos números son:

Por descomposición en factores primos[editar]

Artículo principal: Factorización de enteros

El máximo común divisor de dos números puede calcularse determinando la descomposición en factores primos de los dos números y tomando los factores comunes elevados a la menor potencia, el producto de los cuales será el MCD.

Ejemplo: para calcular el máximo común divisor de 48 y de 60 se obtiene de su factorización en factores primos.

El MCD son los factores comunes con su menor exponente, esto es:

En la práctica, este método solo es operativo para números pequeños tomando en general demasiado tiempo calcular la descomposición en factores primos de dos números cualquiera.

VÍDEO DE NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS

NÚMEROS PRIMOS Y NÚMEROS COMPUESTOS

 En matemáticas, particularmente en teoría de números o aritmética, un número primo es un número naturalmayor que 1 que puede descomponerse solamente en dos factores distintos: él mismo y el 1.^1 2 3 Los números primos se contraponen así a los compuestos, que son aquellos que tienen por lo menos un divisor natural distinto de sí mismos y de 1.

Los números primos menores que 100 son los siguientes: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,47, 53, 59, 61, 67, 71, 73, 79, 83, 89 y 97.⁴

La propiedad de ser primo se denomina primalidad. A veces se habla de número primo impar para referirse a cualquier número primo mayor que 1, ya que este es el único número primo par. A veces se denota el conjunto de todos los números primos por . En la teoría algebraica de números, a los números primos se les conoce como númerosracionales primos para distinguirlos de los números gaussianos primos.⁵

El estudio de los números primos es una parte importante de la teoría de números, rama de las matemáticas que versa sobre las propiedades, básicamente aritméticas, ⁶ de los números enteros. Los números primos están presentes en algunas conjeturas centenarias tales como la hipótesis de Riemann y la conjetura de Goldbach, recientemente resuelta por el peruano Harald Helfgott en su forma débil. La distribución de los números primos es un tema recurrente de investigación en la teoría de números: si se consideran números individuales, los primos parecen estar distribuidos aleatoriamente, pero la distribución «global» de los números primos sigue leyes bien definidas.

Una característica de los números compuestos es que cada uno puede escribirse como producto de dos naturales menores que él. Así, el número 20 es compuesto porque puede expresarse como 4×5; y también el 87 ya que se expresa como 3×29. Sin embargo, no es posible hacer lo mismo con el 17 ó el 23 porque son números primos. Cada número compuesto se puede expresar como multiplicación de dos (o más) números primos específicos, cuyo proceso se conoce como factorización.

El número compuesto más pequeño es el 4 y no hay ninguno que sea mayor que todos los demás; hay infinitos números compuestos.

La forma más sencilla de demostrar que un número n es compuesto, es encontrar un divisor d comprendido entre 1 y n (1 < d < n). Por ejemplo, 219 es compuesto porque tiene a 3 por divisor. Y también 371 porque tiene a 7 por divisor. Sin embargo, este método deja de ser efectivo para números que son producto de primos grandes. Una buena alternativa es utilizar entonces el pequeño teorema de Fermat, o mejor la generalización de este teorema debida al matemático suizo Leonhard Euler.

Como los números primos y compuestos están entremezclados unos con otros es lógico preguntarse si existirán secuencias de números compuestos consecutivos de longitud arbitraria. La secuencia 32, 33, 34, 35 y 36 es un ejemplo de longitud 5, y 114, 115, 116, 117, 118, 119, 120, 121, 122, 123, 124, 125 y 126 un ejemplo de longitud 13. La respuesta es que podemos conseguir una secuencia de números compuestos tan larga como se desee. Si deseamos una secuencia de longitud 20, basta tomar los números 21!+2, 21!+3, 21!+4, ... , 21!+21, ya que el primero es divisible por 2, el segundo por 3, etcétera.

VÍDEO DE MÚLTIPLOS Y DIVISORES DE UN NUMERO

MÚLTIPLOS Y DIVISORES DE UN NUMERO

MÚLTIPLOS Y DIVISORES MÚLTIPLOS DE UN NÚMERO Los múltiplos de un número son los que lo contienen un número exacto de veces. El 12 es múltiplo de 3 porque lo contiene 4 veces. El 30 es múltiplo de 5 porque lo contiene 6 veces. Los múltiplos de un número se calculan multiplicando este número por los números naturales ={0, 1, 2, 3, 4, 5, 6, 7, 8 .......} Los múltiplos de un número son infinitos. Múltiplos de 2={0, 2, 4, 6, 8, 10, 12, 14, 16, 18, 20, 22, 24 ..........} Múltiplos de 3={0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36 ........} Múltiplos de 11={0, 11, 22, 33, 44, 55, 66, 77, 88, 99, 110, 121, 132 ....} MÚLTIPLOS COMUNES A VARIOS NÚMEROS Calculados los conjuntos de los múltiplos de dos o más números siempre podemos encontrar múltiplos comunes. M (3) ={0, 3, 6, 9, 12, 15, 18, 21, 24, 27, 30, 33, 36, 39, 42, 45, 48, 51, 54, 57, 60 ...} M (4) ={0, 4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 42, 44, 48, 52, 56, 60, 64, ....} M (8) ={0, 8, 16, 24, 32, 40, 44, 48, 56, 64, 72, 80, 88 .....} Múltiplos comunes de 3 y 4 ={0,12, 24, 36, 48, 60 ...} Múltiplos comunes de 3 , 4 y 8 ={0, 24, 48.....} Mínimo común múltiplo de varios números (m.c.m.).- Se llama así al menor de los múltiplos comunes de dichos números excluido el cero. m.c.m.(3, 4) = 12 m.c.m.(2, 4, 8)= 24 DIVISORES DE UN NÚMERO Divisor de un número es aquel que está contenido en él un número exacto de veces. Al dividir un número por sus divisores el resto es cero. El 5 es divisor de 15 porque lo contiene tres veces. 15 : 5 = 3 y resto 0. Observa la relación: 5 es divisor de 15 15 es múltiplo de 5 Un número es divisible por otro cuando lo contiene un número exacto de veces. Un número es divisible por todos sus divisores. D (5) = {1, 5} D (6) = {1, 2, 3, 6} D (8) = {1, 2, 4, 8} D (12) = {1, 2, 3, 4, 6, 12} D (20) = {1, 2, 4, 5, 10, 20}

VÍDEO CLASIFICACIÓN Y MEDICIÓN DE ANGULOS

CLASIFICACIÓN Y MEDICIÓN DE ANGULOS

CLASIFICACIÓN Y MEDICIÓN DE ÁNGULOS

NGULOS Cuando dos rectas se encuentran y forman cuatro religiones llamadas ángulos. Cada ángulo esta limitado por dos lados y un vértice. Es la abertura entre dos lados, los cuales tienen un punto común llamado vértice. El lado desde el cual se empieza a medir el ángulo se llama Codo Inicial, y aquel donde se termina se llama Lado Terminal.

Tipos de Ángulos Angulo Convexo: Se llama ángulo convexo R N M a la intersección del semiplano de borde NM, que contiene el punto R, y el semiplano de borde NR, que contiene el punto N.

Angulo Cóncavo: Es el ángulo que se obtiene si consideramos la unión de los semiplanos anteriores.

Ángulos Consecutivos: Son los pares de ángulos que tienen un lado común y ningún otro punto mas.

Ángulo Llano: Cuando los lados de un ángulo son dos semirrectas de una misma recta, el ángulo se llama llano.

Ángulos Rectos: Sean dos semirrectas de origen de un origen común O y supongámoslas prolongadas hasta formar dos rectas, a y b, que se cortan en O y que dividen al plano en 4 regiones a, b, c y d, cada una de ellas correspondiente a un ángulo. Cuando esos cuatro ángulos son iguales, se dice que cada uno de ellos es un ángulo recto y que sus lados son perpendiculares.

Angulos Oblicuos: Las rectas que se cortan formando ángulos desiguales se llaman oblicuas. A estos ángulos que no son rectos se les llaman oblicuos.

•Agudos: Si son menores que un recto.

•Obtusos: Si son mayores que un recto.

MEDIDA DE ANGULOS

Para medir ángulos se emplean fundamentalmente dos sistemas: el que utiliza como unidad el grado sexagesimal y el que utiliza como unidad el radián.

Medición de ángulos

Medir un ángulo es compararlo con otro que se toma por unidad de medida. Para medir los ángulos existen varios sistemas, siendo los más conocidos el sistema sexagesimal y el circular.

Sistemas de medidas angulares

Sistema Sexagesimal: en éste sistema la unidad de medida es el grado sexagesimal que corresponde a que se abrevia 1°; éste a su vez se divide en 60 partes iguales y corresponde a un minuto sexagesimal que se abrevia ; éste a su vez se divide en 60 partes iguales y corresponde a un segundo sexagesimal que se abrevia .

Sistema Circular: en éste sistema la unidad de medida es el radian.

¿Qué es el radian?: El radian es un ángulo central que tiene como lados 2 radios de una circunferencia, cuyo arco es igual al radio de la circunferencia al cual pertenece.

Siendo;  = 3,141592654

R = 1

Las unidades de medida que pasaré a estudiar pertenecen al sistema sexagesimal y circular.

Equivalencia entre los sistemas

Ángulos Complementarios: Son los que miden 90º.

Ángulos Suplementarios: Son los que miden 180º

LONGITUD DE ARCO

Si ө es un ángulo central que mide un radian entonces la longitud del arco subtendido es igual al radio ®. Donde r es la longitud del radio.

Cuando en ángulo Ө mide 2 radianes, entonces la longitud del arco subtendido mide 2 r.

De manera general si el ángulo mide + radianes entonces la longitud de arco subtendido mide + r.

fuente de referencia:

VIDEO DE LA AREA DEL PORALELOGRAMO

ÁREA DEL PARALELOGRAMO

• aralelogramos rectángulos, son aquellos cuyos ángulos internos son todos ángulos rectos^{[cita requerida]}. En esta clasificación se incluyen ² :
  • El cuadrado, que tiene todos sus lados de igual longitud.
  • El rectángulo, que tiene sus lados opuestos de igual longitud.

• Paralelogramos no rectángulos, ^{[cita requerida]}son aquellos que tienen dos ángulos internos agudos y dos ángulos internos obtusos. En esta clasificación se incluyen:
  • El rombo, que tiene todos sus lados de igual longitud, y dos pares de ángulos iguales.
  • El romboide, que tiene los lados opuestos de igual longitud y dos pares de ángulos iguales.

Por otra parte podemos clasificar a los paralelogramos en polígonos equiláteros y no equiláteros, con lo que tenemos:

• Paralelogramos equiláteros, con sus cuatro lados iguales:
  • El cuadrado, que tiene todos sus lados de igual longitud (y todos sus ángulos rectos).
  • El rombo, que tiene todos sus lados de igual longitud (pero sus ángulos no son rectos).

• Paralelogramos no equiláteros, si sus cuatro lados no son iguales:
  • El rectángulo, en el que solo sus lados opuestos tienen igual longitud (y todos sus ángulos son rectos).
  • El romboide, en el que solo los lados opuestos son iguales (y sus ángulos no son rectos).

VIDEO LA DIVISION

DIVISIÓN DE NÚMEROS NATURALES

DIVISIÓN DE NÚMEROS NATURALES

n matemática, la división es una operación parcialmente definida en el conjunto de los números naturales y los números enteros; en cambio, en el caso de los números racionales, reales y complejos es siempre posible efectuar la división, exigiendo que el divisor sea distinto de cero, sea cual fuere la naturaleza de los números a dividir. En el caso de que sea posible efectuar la división, esta consiste en indagar cuántas veces un número (divisor) está "contenido" en otro número (dividendo). El resultado de una división recibe el nombre decociente. De manera general puede decirse que la división es la operación inversa de la multiplicación, siempre y cuando se realice en un campo.¹

Debe distinguirse la división «exacta» (sujeto principal de este artículo) de la «división con resto» o residuo (la división euclídea). A diferencia de la suma, la resta o la multiplicación, la división entre números enteros no está siempre definida; en efecto: 4 dividido 2 es igual a 2 (un número entero), pero 2 entre 4 es igual a 1/2 (un medio), que ya no es un número entero. La definición formal de «división» , «divisibilidad» y «conmensurabilidad», dependerá luego del conjunto de definición.

VÍDEO ADICIÓN Y SUSTRACCIÓN DE NÚMEROS NATURALES

ADICIÓN Y SUSTRACCIÓN DE NÚMEROS NATURALES

ADICIÓN Y SUSTRACCIÓN DE NÚMEROS NATURALES 

En matemáticas, un número natural (designado por ℕ) es cualquiera de los números que se usan para contar los elementos de un conjunto como también en operaciones elementales de cálculo.

Por definición convencional se dirá que cualquier miembro del siguiente conjunto, ℕ = {0, 1, 2, 3, 4, …} es un número natural, que en este caso empieza del cero y prosigue ad infinitum. De dos números vecinos cualesquiera, el que se encuentra a la derecha se llamasiguiente o sucesivo ¹ .

El conjunto de todos los números naturales iguales o menores que cierto número natural  se llama segmento de una sucesión natural y se denota 

VIDEO VALOR POSICIONAL Y LECTURA DE LOS NÚMEROS NATURALES

VALOR POSICIONAL Y LECTURA DE NUMEROS NATURALES

LOS NÚMEROS NATURALES NUESTRO SISTEMA DE NUMERACIÓN (Características)  Es decimal porque diez unidades de un orden forman una unidad del orden inmediato superior. 10 U = 1 D 10 D = 1C 10C = 1 UM  Es posicional porque el valor de una cifra depende de su posición en el número. Millares de millón Millones Millares Unidades CmM DmM UmM Cm Dm Um CM DM UM C D U Los números los podemos descomponer indicando la suma de sus diferentes órdenes, o bien, la suma del valor posicional de sus cifras. 21403.745 = 2 Um + 4 CM + 0 DM + 3 UM + 7 C + 4 D + 5 U 21403.745 = 21000.000 + 400.000 + 3.000 + 700 + 40 + 5 LECTURA Y ESCRITURA DE NÚMEROS: - Para leer o escribir con palabras un número se empieza por la izquierda leyendo o escribiendo: - El grupo de los millones. - El grupo de los millares. - El grupo de las unidades. Si algún grupo tiene ceros no se nombra. 231204.329 = Veintitrés millones doscientos cuatro mil trescientos veintinueve. 41000.207 = Cuatro millones doscientos siete. 47.002.000 Cuarenta y siete millones dos mil. COMPARACIÓN Y ORDENACIÓN DE NÚMEROS: Para ordenar números nos fijamos:  Número de cifras: Mayor el que más cifras tiene. 15.312  5 cifras 5.980  4 cifras 117.920  6 cifras El mayor será 117.920 que posee 6 cifras y el menor 5.980 que posee 4 cifras.  Valor de cada cifra; Si los números poseen el mismo número de cifras empezando por la izquierda vamos comparando cifra a cifra. Los números 24.243 y 26.115 tienen el mismo número de cifras, así que empezaremos a comparar los valores de sus cifras empezando por la izquierda. Vemos que la cifra de las decenas de mil la misma, 2, así que comparamos la siguiente cifra, las unidades de mil, que en el primer número es 4 y en el segundo es 6. Por lo tanto el número mayor es el segundo, el 26.115  Para comparar utilizamos los símbolos: > Mayor que < Menor que = Igual que 117.920 > 15.312 > 5.980 (Ordenados de mayor a menor) 5.980 < 15.312 < 117.920 (Ordenados de menor a mayor)

 

Para saberlo se puede identificar visualmente o mediante el conteo. Para ello, la persona debesaber el nombre de los números.Los primeros números naturales son 1, 2, 3, 4, 5, 6, 7, 8 y 9. Estos también se llaman dígitos. Alcombinarlos se puede formar cualquier número natural.Valor absoluto y valor relativoCada dígito tiene dos valores: el absoluto y el relativo.Valor absoluto:Se refiere al número que representa, es una constante, no cambia.Por ejemplo:5 + + + + + 4 + + + + 6 + + + + + +El valor absoluto corresponde a su valor como número natural; por ejemplo, el tres en elnúmero 456 132 representa tres unidades.Valor relativo:Se refiere al lugar que ocupa.

C D U

55 05 0 0El valor relativo en la misma cantidad es el que adquiere por su posición en la cifra. En el casodel número 456 132, el 3 vale 30 unidades, porque se encuentra en el lugar de las decenas, deacuerdo con nuestro sistema decimal de notación de los números, que es posicional.Sistema decimal:Es el que utilizamos regularmente, en donde cada número, de acuerdo con su posición tieneun valor relativo igual a diez veces del que está a su derecha.Por ejemplo:Para el número 325